Phyllotaxis

Phyllotaxis is the study of the successive arrangement of radial parts of a growing plant, such as the leaves on a stem, or the seeds in the head of a sunflower. Some examples from nature can be seen here.

Essentially, these arrangements cen be generated using the following simple procedure. Imagine the first leaf coming off of the stem of some plant. The second leaf that grows from the stem will, first of all, be further outwards or further up the stem, and second of all, it will be coming off of the stem at a different angle than the first leaf. The third leaf then does the same as the second. It grows further outwards or further up the stem than the second did, and the angle at which it grows has increased again by the same amount it did between the first and the second leaves. That is the procedure for generating a phyllotaxic arrangement of leaves, or other things.

This application generates a simple phyllotaxic arrangement of circles, expanding outward at either a linear or an exponential rate. You can specify the angle between each circle (between 0 and 360 degrees), and you can determine rate of expansion using a pair of slider controls. See figure A. Animated transitions between phyllotaxis arrangements which differ in their angle, or their exponential rate, or both, can be created using another corresponding pair of buttons to the left of the slider controls for angle and expansion rate. See Figure A. The animation speed and the lower and upper bounds for the angle and expansion rate slider controls can be set in a control panel dialog accessible from the Controls menu.

Figure A

At the heart of my motivation for creating this application was the following thought. It can be observed that many plants are employing particular phyllotaxic arrangements of leaves in which the amount of leaf surface area which is open to sunlight is maximized. Conversely, if it is not the surface area of leaves open to sunlight that the plant hopes to maximize, but it is instead the volumetric space in the head of a sunflower, for instance, then it is still naturally the case that certain phyllotaxic arrangements will provide more volumetric space for each of the seeds than will other arrangements. This all given, and given that the leaves or sunflower seeds are appearing one after another starting from the inside and moving in an outward direction, and given that the seeds will grow to be as large as they can in their naturally determined spaces, it seems clear that in a phyllotaxic arrangement with a particular angle and rate of outward growth, the maximum size of any seed is going to be limited by one other neighboring seed. And if the successive seeds are numbered, then what is the position in the sequence of the seed which is limiting the maximum size of the n^th seed in the sequence of a particular phyllotaxic arrangement? But most interesting of all is that, as either the angle between successive seeds, or the rate of expansion between successive seeds, changes very gradually, at what points (at what combination of values of angle and expansion rate) is there an instantaneous change between which seed in the seqence is limiting the maximum size of the n^th seed? In order to answer this question, as the application draws a particular phyllotaxic arrangement of circles, it maximizes the size of each circle starting from the inside and moving outward, making each circle in the sequential arrangement as large as it can be without intersecting any other circle. Furthermore, lines can be drawn between the n^th circle and the circle which is limiting the size of the n^th circle, creating a set of spiral "bond" lines. Notice that these spirals change direction at key points. The interval in the phyllotaxic sequence between the n^th circle and the circle which is limiting the size of the n^th circle is displayed at the bottom of the area of the screen for the angle and expansion rate slider controls.

• Application features
• Author

Phyllotaxis application features

• Drawing options.
  
  
  1. Number the successive circles in the arrangement
  2. Connect the circles' centers with lines instead of drawing solid circles
  3. Draw a set of spiral "bond" lines which indiciate which neighboring circle is limting the maximum size of a particular circle.
     
     
• Graphing options.
  
  
  1. Graph showing radius of each of the successive circles in the phyllotaxic arrangement.
  2. Graph showing density of space (measured as the fraction of space which is contained in the interior of the circles; that is, the fraction of space which is occupied by the the area of the circles) as the radius of the density sample increases. Just curious to see if the density was constant.
     
     
• Other features
  
  
  1. You can print an image of any phyllotaxis arrangement of any size. The image will be broken down into many pages, if necessary, which you can fasten together somehow. I recommend that you make sure that no graphs and none of the controls are showing when you print.
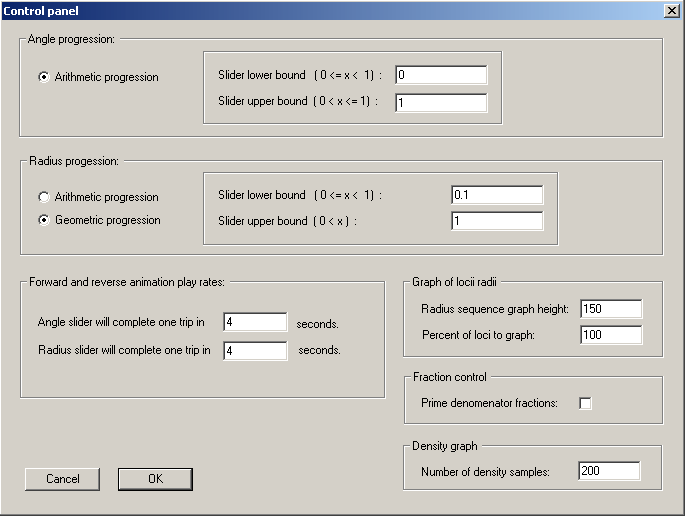
  2. There is a control panel, accessible from the Controls menu, from which you specify whether the expansion rate for the phyllotaxis arrangement is linear or exponential, where you can set the lower and upper bounds for each of the angle and expansion rate slider controls, specify durations for the individual animations, and specify some things about the graphs. See Figure B.
     
     
     
     
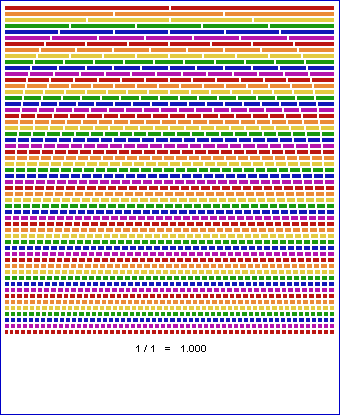
  3. There is a curious and pretty useless control which I made for specifying fractional values for the angle of a phyllotaxic arrangement. See Figure C. The idea is that the first row of thin colored bars, which has 2 red bars, is for specifying halves.  The second row is for specifying thirds, the fourth row for fourths, etc. You simply have to click on one of the bars, or click and drag to see a set of phyllotaxic arrangements with those angles between circles, where one-half means one-half of a circle or 180 degrees.
     
     Figure C
     
     

Author

Please share your thoughts, criticisms, questions, and bug reports with me. Hope you enjoyed this application.

Brian DiLoreto

brian_diloreto@yahoo.com