Depicted here are the polyhedra whose vertices have repelled each other on the surface of a sphere, until their positions have stabilized. The simplest such polyhedron has 4 vertices, and naturally becomes a tetrahedron. The remaining polyhedra, with an integral number of vertices, are NOT regular polyhedra. I call them "quantum hulls" because they are all convex hulls with triangular faces, and the number of vertices is quantized.
When the consecutive polyhedra are made to be concentric, with the tetrahedron being the innermost hull, and each hull is able to rotate freely about its center, then it is interesting to see the dynamics that occur when the vertices of each hull attract or repel the vertices of the adjacent, outer concentric hull. By rotating the innermost hull, all outer hulls are affected in turn, and their orientations change to find the lowest energy state, where the repulsive or attractive forces are minimized.
Screenshot:
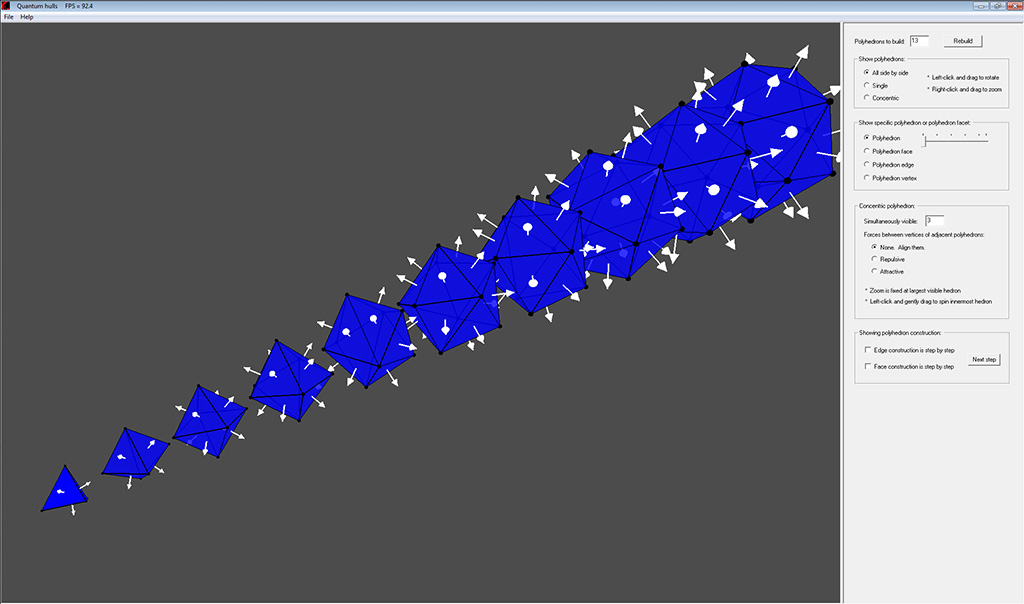
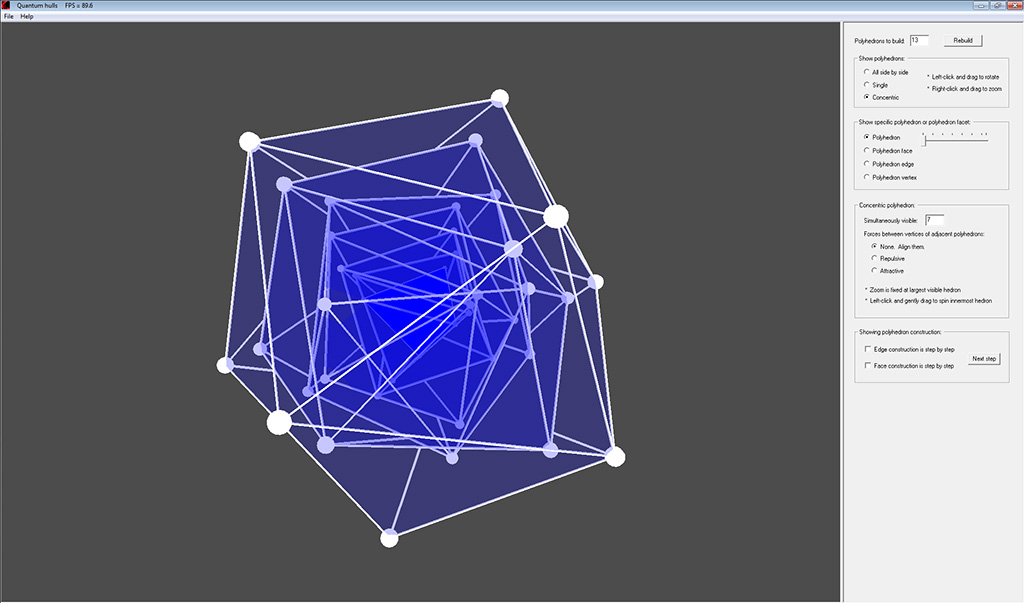
Copyright © 2023 Atomic Concepts Software