by Brian DiLoreto
The Golden Mean or Golden Ratio, represented by the Greek letter ø (phi), is one of those mysterious natural numbers, like e or pi, that seem to arise out of the basic structure of our cosmos. Phi is often called the Golden Ratio since it describes a relationship, or ratio, between consecutive members of some sequence, such as the ratio of sizes of successive leaves of a plant.
Phi's nature as a ratio of sizes can be seen from the following simple definition. Break a line segment into two parts such that the ratio of the whole to the longer segment is the same as the ratio of the longer segment to the shorter segment. See figure A.
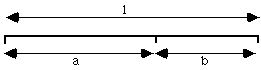
This condition can expressed as 1 / a = a / b, or equivalently, 1 / a = a / (1-a) since b = (1-a), which can be further reduced to the quadratic equation a2 + a - 1 = 0. Solving the equation for a yields the decimal value 1.6180339887499..., suggesting that in a sequence governed by the ratio phi, successive members of the squence will have the ratio 1.6180339887499.... That is, any member of the sequence will be 1.6180339887499 times as big as the member before it. The Fibonacci sequence, in which each member of the sequence is the sum of the previous two terms is governed by phi. The Fibonacci sequence begins with 1,1, and so the remainder of the sequence begins 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... The ratio of successive terms in this sequence (for example 8 / 5 = 1.6) approaches phi more and more closely the further down the sequence one goes.
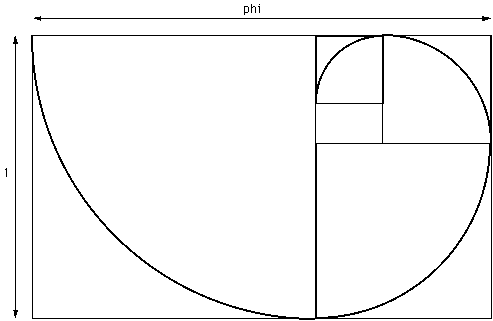
An alternative definition of phi can be found by trying to find a rectangle of the proper dimensions such that when a square is removed, the remaining rectangle has the same proportions as the original, larger rectangle. See figure B, comparing the largest rectangle to the next largest rectangle, which is inside of the first. The only rectangle whose dimensions satisfy this problem is a rectangle in which the ratio of its sides is phi. That is, if the shorter side of the rectangle is equal to 1 unit in length, then the longer side of the rectangle will have a length that is 1 * phi units in length. This "golden rectangle" is the 2-dimensional version of the original, 1-dimensional definition of phi above.
Because the remaining rectangle in the figure below has the same the same proportions as the original rectangle, the process of dividing a rectangle into a square and a left-over rectangle can be continued indefinitely, each successive embedded rectangle being smaller than the last. If circular arcs are drawn within each of the square sections, a logarithmic or equiangular spiral is created since each embedded rectangle is turned 90 degrees from the previous. Spirals such as these occur frequently in nature in shells, sunflowers, and pine cones.
Naturally one might wonder if there is a 3-dimensional "golden rectangular solid", analagous to the 2-dimensional "golden rectangle", which can be sub-divided indefinitely so that each left-over rectangular solid has the same proportions as the original solid. The 3D analogue to the 2D golden rectangle does indeed exist, and is depicted by this application. Note that because there are now 3-dimensions involved, each rectangular solid which is embedded, or contained, within a larger rectangular solid has been turned 90 degrees in two perpendicular directions with respect to the larger rectangular solid.
All other controls are located in the control panel at the right of the screen. See figure C.
The first group of controls in the control panel is contained within a box labeled 'Embedding orientation'. There are four possible orientations in 3-dimensional space that each rectangular solid can have with respect to the larger rectangular solid in which it is embedded. In the 2-dimensional "golden rectangle", each embedded rectangle can be oriented in only two different ways. Involving the 3rd dimension provides for an additional degree of freedom, and consequently doubles the number of possible orientations in space in which each embedded rectangular solid can situated. Presumably, if there was an analagous 4-dimensional "golden rectangular hypersolid", each hypersolid could be oriented in 8 different ways with respect to the hypersolid in which it is embedded.
NOTE: The Golden spiral curve, discussed in a moment, will appear as a thick tube instead of a line only when the embedding orientation is 'A'. This is the primary embedding orientation since the curve need not stray outside of any of the rectangular solids.
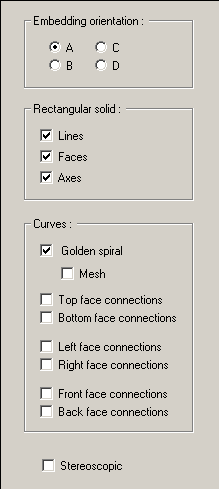
The second group of controls, contained in the box labeled 'Rectangular solid' determine what parts of each rectangular solid are rendered. The edges (lines), the faces, and the axes defining the orientation of each of each rectangular solid can be drawn.
The third group of controls, contained in the box labeled 'Curves' determines what curves will be drawn. The "golden spiral" curve is the main curve of interest and is analagous to the logarithmic spiral of the 2-dimensional "rectangular solid" seen in figure B. It passes through the corner of each rectangular solid which acts as the orientation reference. Checking the box labeled 'mesh' will cause the golden spiral curve to be drawn as a net of lines instead of an opaque tube. Note that the "golden spiral" curve will appear as an opaque tube, or a mesh tube, only when the embedding orientation is 'A'. Otherwise, it will appear as a curved line.
The remaining checkboxes in the 'Curves' groupbox cause curves to be drawn which connect the top, bottom, left, right, front, and back faces of consecutively embedded rectangular solids.
At the very bottom of the control panel is a checkbox labeled 'Stereoscopic'. Checking this box causes two separate images of the scene to be rendered, one in red for the left eye, and one in blue for the right eye, providing a true 3-dimensional scene when viewed with standard 3D red-blue glasses.
Hope you enjoy this software.
Any thoughts, comments, suggestions, criticisms can be directed to me at brian_diloreto@yahoo.com
Thanks.
Brian DiLoreto 3/14/2002